グラブルが確率を偽って景品表示法に違反しているだとか、To LOVEるのガチャの確率が異様に低いとか世の中ソーシャルゲーム内に設置されれているガチャで騒ぎが起きているようです。
その確率で、実際にどれくらいガチャを引けば当たるのか、少し気になります。
ただ、一介のサラリーマンがウン十万を課金して体当たりで確率を確かめる訳にはいかないので、今回は、プログラミングで確かめてみたいと思います。
以下、別に大学で確率を勉強したわけじゃないので、体当たり的にやっていこうと思います。
条件
今回検証するにあたっての条件です。
- 100, 1000, 1万, 10万分の1を対象にします。(1回あたり)
- 10万~1000万人のユーザーが当たるまでガチャを引きまくります。
- 全員当たらないからと言って途中であきらめたりしません。
- 運営による途中での確率操作はありません。
- ガチャは1回300円で引けます。
- 計算の実行は1度のみです。
- 乱数はc#のRandumクラスで作ります*1
100分の1 (0.01%)
当たる確率が100分の1のガチャを10万人で引きまくって当たった人から抜けていきます。
やる前に想定してる事
- 100分の1なら100回やれば必ず当たるんでしょ!!!
- 100回かそこらを中心に正規分布っぽい山ができるんでしょ!!!
では、やってみたいと思います。
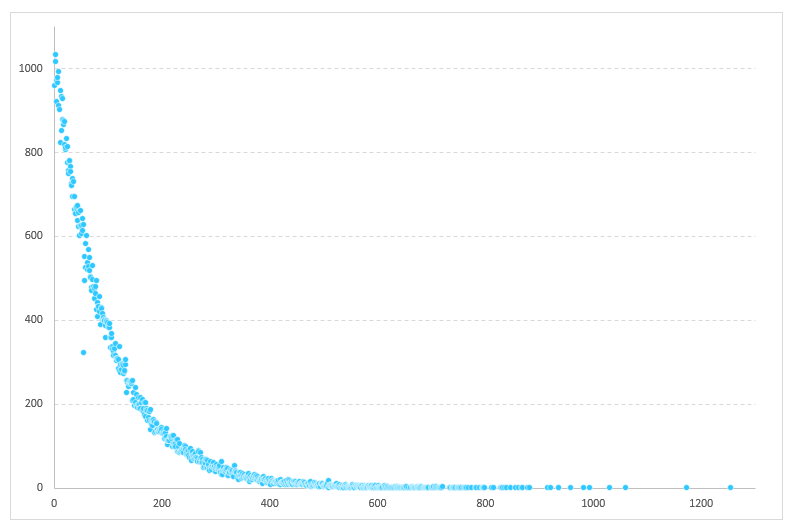
・・・・・ん?
意外な結果が出ました。
何らかの正規分布になるかと思ってたけど1回で当たる奴多いな!
1回が最大で右肩下がりになりました。自分の計算が間違っていないか少々不安です。
最小の1回で当たった人が960人もいましまた。
最大は1255回引いてやっと当たった人が1人います。37万6千5百円課金してしまったようです。
100分の1で1255回ひいてやっと当たるって不運ってレベルじゃないですね。
1000分の1 (0.001%)
今度は1,000分の1です。
まずは結果から。
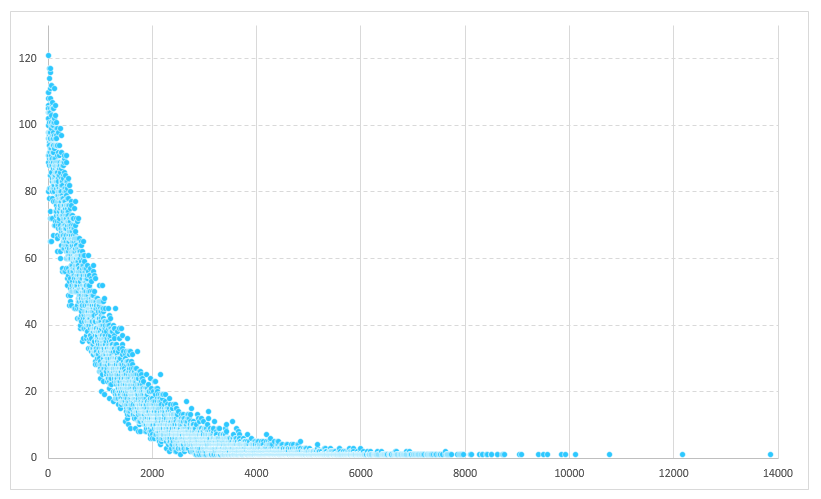
さっきと同じような結果になりました。
同じように正規分布は見られません。
今回も1回で当たる人が結構いますね。
1回で当たった人は105人
最大は、13860回引いてやっと当たった人が1人います。課金額にすると415万8千円でした。
途中で血の涙を流しながら引いている姿が想像できますね。
1万分の1 (0.0001%)
試行回数が少ないとグラフが綺麗に出ないので今回は100万人にガチャを引いてもらおうと思います。オンボロPCなので計算が終わるかどうかが危ぶまれます。
やばい・・計算に15分もかかりました。
では、まずは結果から。
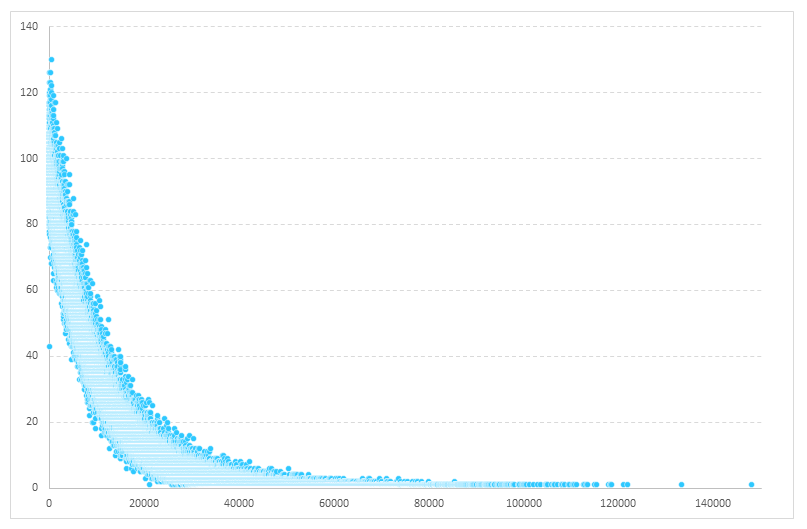
え、マジで?!
この確率でも1回で引いてしまう人がでました。
1回で当たった人は93人
最大は、147993回引いてやっと当たった人が1人います。課金額にすると44,397,900、なんと4千4百万円かかりました。
1万分の1で14万7千回もガチャを引かせるとはさすが運営(誰)。やることがエグいですね。
この人もう、神を呪うレベルの不運じゃないでしょうか。
10万分の1(0.00001%)
ここまでくるともう、ガチャ界では前人未到の確率です。
ToLoveるのガチャですら20万分の13(0.00065%)なのでそれより更に65倍(合ってるよね?)当たらない計算です。
正直、10万分の1のガチャなんて知ってたら引く気が一切起きないですね。
中の人は感覚がマヒしてそうなので、そのうち平気でこれくらいやってきそうな気がします。
しかしさすがに、ギャンブルでもないのにこの確率は強烈すぎます。
まぁだからと言って確率を表示しないという選択をすると今度は景品表示法さんではなく、風営法さんがアップし始めそうですね。
さて、前置きが長くなりましたが、これを1000万人の方に引いてもらいます。
・・・・計算するのに人力マルチスレッドで4時間かかりました。
では結果です。
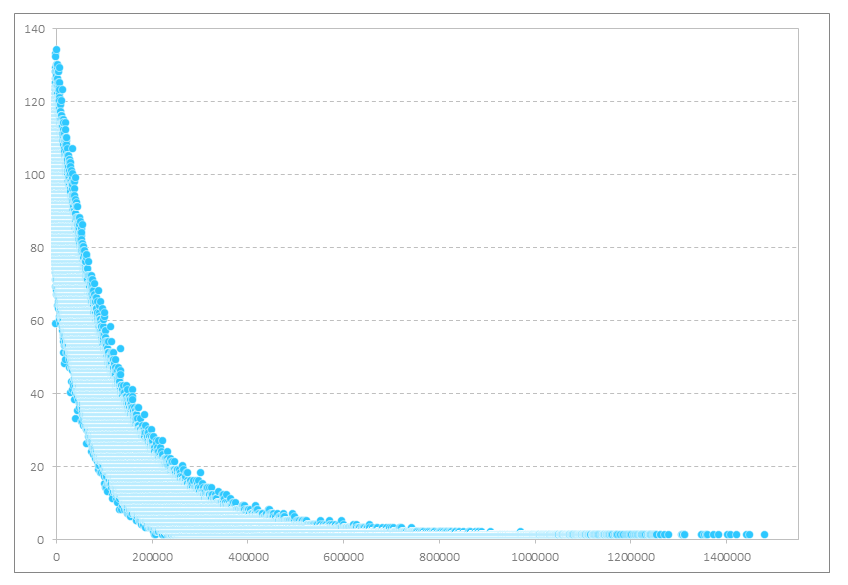
傾向は同じですが、数字の桁がおかしいですね。
どうやら、流石になかなか当たらないみたいです。
が、やっぱり1回で当たる超運の持ち主がいますね。
1回で当たった人は103人
最大は、148万2305回引いてやっと当たった人が1人います。課金額にすると444,691,500円で、なんと4億4469万円かかりました。
10万分の1で148万回・・?
仏教での罪人の扱いに近いんじゃないでしょうか?
使ったコード
今回実験に使ったコードを以下に置いておきます。
/// <summary> /// メインクラス /// </summary> internal static class AppMain { /// <summary>乱数生成器</summary> private static Random r = new Random(); /// <summary> /// メインメソッド /// </summary> private static void Main(string[] args) { // ガチャを引く人数 int person = 100000; // 当たる確率 int odds = 100000; // ulong型は1000京以上カウント可能 var result = new List<ulong>(); for (int i = 0; i < person; i++) { result.Add(TryGacha(odds)); } // 全員の当たった回数を出力 AppMain.Write(@"d:\result.csv", AppMain.countWinner(result)); Console.WriteLine("Finished."); Console.ReadLine(); } /// <summary> /// 当たるまでガチャを引く /// </summary> /// <param name="max">確率を表す整数</param> /// <returns>当たるまでの回数</returns> public static ulong TryGacha(int max) { ulong result = 1; int ans = r.Next(0, max); // 当たりのランダム化 while (true) { if (r.Next(0, max) == ans ) { break; } result++; } return result; } /// <summary> /// 当たった回数ごとの人数を集計します。 /// </summary> public static IDictionary<ulong, int> countWinner(IList<ulong> list) { var table = new SortedDictionary<ulong, int>(); foreach (var item in list) { if (!table.ContainsKey(item)) { table[item] = 0; } table[item]++; } return table; } /// <summary> /// 結果をCSV形式で書き出す /// </summary> public static void Write(string path, List<ulong> result) { using (var file = File.Create(path)) using (var sw = new StreamWriter(file)) { for (int i = 0; i < result.Count; i++) { sw.WriteLine(result[i]); } } } /// <summary> /// 結果をCSV形式で書き出す /// </summary> public static void Write(string path, IDictionary<ulong, int> table) { using (var file = File.Create(path)) using (var sw = new StreamWriter(file)) { foreach (var item in table) { sw.WriteLine(item.Key + ", " + item.Value); } } } } // class end.
まとめ
初回が一番高くだんだん下がることが分かって意外な感じでした。
これを書いてる途中にあるソシャゲは3人で課金が全体の7割りとかグラブルは連続でガチャを回すひとの確率は絞るとか聞こえてきましたが、中の人はぜひ当たらない人の救済をしてほしいものですね。
- N分の1だからってN回引いて当たるとは限らない
- ものの数回で当たる奴は集計の母体が大きいと必ず居る
- 100分の1なら10回、1000分の1なら100回(=N分の1の10倍で5~6割の人が当たる)
- 運が悪いとN分の1のNの15倍引かないと当たらないこともある
でした。
*1:このクラスの乱数生成に十分な性能があると想定して実行します